TPU本构模型
Feb 27, 2017 • 1 min read
Thermoplastic polyurethane（TPU）是一种高分子材料，常用于制造手机保护壳。材料性能介于较硬的橡胶和较软的塑料之间。去年刚来新加坡的时候做了一段时间的TPU本构模型研究，该材料由硬的和软的两相组成，因而在循环载荷的作用下呈现出独特的力学行为：
- 滞回环，即加载时的应力应变曲线与卸载的时候不同，表明了存在能量的损失；
- 塑性变形，即在完全卸载之后材料还存在一些未恢复的变形；
- 加载率相关，即材料的力学行为与加载速率相关，加载率大，所得应力也高，这说明了存在粘性；
- 应力软化，即后续循环的应力较初次循环的要小。
Qi-Boyce 本构模型
为了能模拟上述这些力学行为，Qi 和 Boyce 提出了一种TPU本构模型，如图2所示。左侧的超弹性弹簧代表的硬的相，而右侧的线弹性弹簧和阻尼则代表软的相。由于右侧的元素在变形之后会出现粘性松弛，而且在无限长时间后会完全松弛，即应力为0。由此可知，左侧的元素描述的是材料平衡状态或是稳定状态。此三元素使得描述前三个行为成为可能，最后的应力软化体现在两相之间的转换，确切的说法是在循环加载之后软的相增多。
在大变形情况下，采用变形梯度 $F$ 来描述变形，应力通常用Cauchy应力 $T$ 来描述。
\begin{equation*}
F=F^N=F^V \\
F^V=F^{Ve}=F^{Vv} \\
L^V=\dot{F}^V(F^V)^{-1}=\dot{F}^{Ve}(F^{Ve})^{-1}+F^{Ve}\dot{F}^{Vv}(F^{Vv})^{-1}(F^{Ve})^{-1} \\
L^{Ve}=\dot{F}^{Ve}(F^{Ve})^{-1} \\
L^{Vv}=\dot{F}^{Vv}(F^{Vv})^{-1}=D^{Vv}+W^{Vv} \\
W^{Vv}=0 \\
\dot{F}^{Vv}=D^{Vv}F^{Vv}
\end{equation*}
\begin{equation*}
T=T^N+T^V \\
T^N=\frac{\mu_rv_sX}{3J^N}\frac{\sqrt{N}}{\Lambda_{chain}}\mathscr{L}^{-1}(\frac{\Lambda_{chain}}{\sqrt{N}}){\bar{B}^\prime} \\
\mathscr{L}(\beta)=coth(\beta)-\frac{1}{\beta} \\
X=1+3.5(1-v_s)+18(1-v_s)^2 \\
J^N=det(F^N) \\
\bar{F}^N=(J^N)^{-1/3}F^N \\
\bar{B}=\bar{F}^N(\bar{F}^N)^T \\
{\bar{B}^\prime}=dev(\bar{B})=\bar{B}-\frac{1}{3}tr(\bar{B})I \\
\bar{I}_1=tr(\bar{B}) \\
\lambda_{chain}=\sqrt{\bar{I}_1/3} \\
\Lambda_{chain}=\sqrt{X(\lambda_{chain}^2-1)+1} \\
\dot{v}_s=A(v_{ss}-v_s)\frac{\lambda_{chain}^{lock}-1}{(\lambda_{chain}^{lock}-\Lambda_{chain}^{max})^2}\dot{\Lambda}_{chain}^{max} \\
\lambda_{chain}^{lock}=\sqrt{N}
\end{equation*}
\begin{equation*}
\dot{\Lambda}_{chain}^{max}=\begin{cases}
0 & \Lambda_{chain} \lt \Lambda_{chain}^{max} \\
\dot{\Lambda}_{chain} & \Lambda_{chain} \ge \Lambda_{chain}^{max}
\end{cases}
\end{equation*}
\begin{equation*}
T^V=\frac{v_h}{J^{Ve}}\mathbf{L}^e[lnV^{Ve}] \\
J^{Ve}=det(F^{Ve}) \\
D^{Vv}=\frac{\dot{\gamma}^V}{\sqrt{2}\bar{\tau}^V}{\bar{T}^V}^\prime \\
{\bar{T}^V}=(R^{Ve})^TT^VR^{Ve} \\
{\bar{T}^V}^\prime=dev(\bar{T}^V) \\
\bar{\tau}^V=[\frac{1}{2}{\bar{T}^V}^\prime{\bar{T}^V}^\prime]^{1/2} \\
\dot{\gamma}^V=\dot{\gamma}_0exp[-\frac{\Delta G}{k\Theta}(1-\frac{\bar{\tau}^V}{s})] \\
s=\frac{v_h}{v_{h0}}s_0
\end{equation*}
需要说明的是，$F^{Ve}$ 和 $F^{Vv}$ 分别代表的是线弹性弹簧和阻尼的变形梯度。$v_s$ 和 $v_h$ 分别代表的是软的相和硬的相的比例，$v_s+v_h=1$。在加载情况下，$\Lambda_{chain}$ 不断增加，使得 $v_s$ 不断增加，而 $X$ 则减小，在加载峰值时 $\Lambda_{chain}^{max}$ 被记录下来，而在卸载阶段，$v_s$ 保持不变。故而在下次加载时，$v_s$ 和 $X$ 两者的共同作用使得应力 $T^N$ 变小。其实在加载过程中，其应力也是减小的，这是相对于不考虑两相转化时的情况，即 $T^N$ 的表达式中没有 $v_s$ 和 $X$。如果第二次加载时最大载荷保持不变，那么第二次加载之后 $T^N$ 就稳定了。但由于粘性使得 $F^{Ve}$ 可能有变化，总应力或许有变化有待查证。其中的材料参数有 $E$，$v$，$\mu_r$，$N$，$A$，$v_{s0}$，$v_{ss}$，$s_0$，$\dot{\gamma}_0$，$\Delta G$。
由于 $L^{Vv}$ 是在松弛状态下的变形率，其驱动力也应该是在松弛状态下的应力。但 $T^V$ 是当前状态下的 Cauchy 应力，需要进行转换，${\bar{T}^V}=(R^{Ve})^TT^VR^{Ve}$。这一点很重要，涉及到了在两种状态下各变量的转换问题，初学者不易掌握。
VUMAT 实现方法
在VUMAT中，已知的是当前时刻以及下一个时刻的变形梯度 $F_{n}$ 和 $F_{n+1}$，重点是计算 $F^{Vv}$ 和 $v_s$，两者都可以采用4阶龙格库塔法来求解。详细来说，$v_s$ 只和 $F_{n+1}$相关，所以可以直接根据积分或是4阶龙格库塔法来求解。而对于 $F^{Vv}$，则需要将总的变形梯度分为两部分，前一部分为 $F^{Ve}$，决定了线弹性弹簧的应力，该应力控制了 $F^{Vv}$ 的变化率，所以只能采用4阶龙格库塔法来求解。
\begin{equation*}
\dot{F}^{Vv}=D^{Vv}F^{Vv}=f(F^V,F^{Vv}) \\
k_1=f(F^V_n,F^{Vv}_n) \\
k_2=f(F^V_{n+1/2},F^{Vv}_n+k_1*\frac{dt}{2}) \\
k_3=f(F^V_{n+1/2},F^{Vv}_n+k_2*\frac{dt}{2}) \\
k_4=f(F^V_{n+1},F^{Vv}_n+k_3*dt) \\
F^{Vv}_{n+1}=F^{Vv}_{n}+(k_1+2*k_2+2*k_3+k_4)*\frac{dt}{6} \\
F^V_{n+1/2}=(F^V_{n}+F^V_{n+1})/2
\end{equation*}
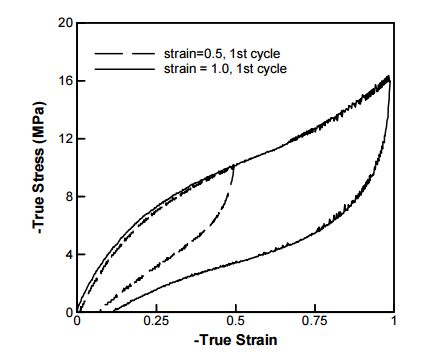
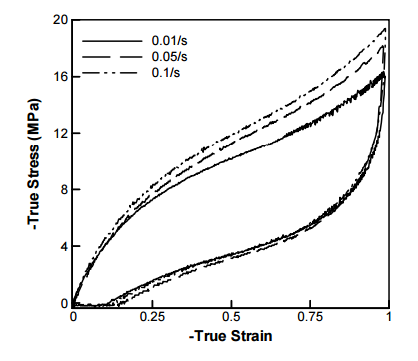
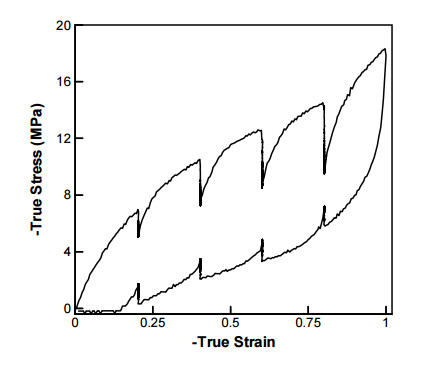
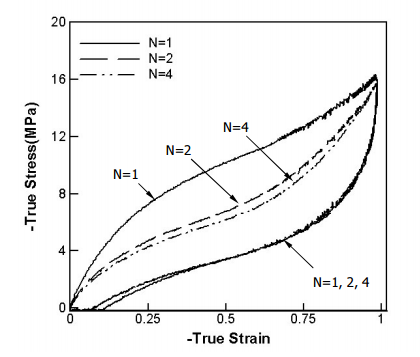
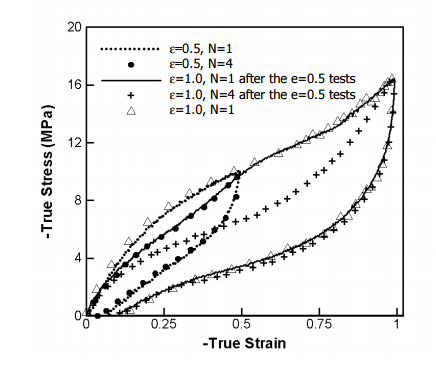TPU循环应力应变曲线
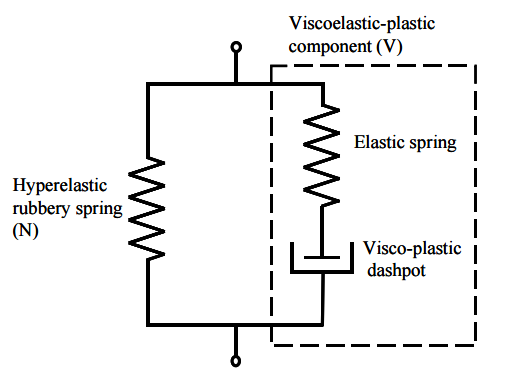TPU本构模型
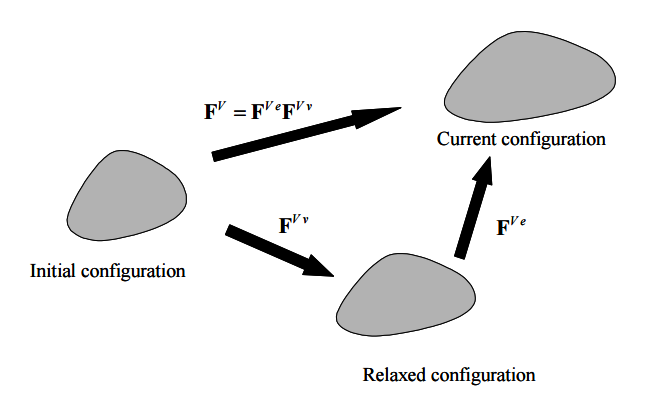变形梯度 $F^V$ 的分解