Shen
Cover image

Arruda-Boyce本构模型

Feb 28, 2017 • 1 min read

在介绍 Arruda-Boyce 本构模型简称 AB 模型之前，我先简单介绍下 MC Boyce 吧。上图中的 Boyce 看起来很和蔼，年轻时必定是个大美女。扯远了，她绝对是个力学大牛，尤其是在高分子材料力学行为研究这一块，感觉无人能出其右。现在我们使用的高分子材料本构模型大部分出自其手，上一篇博客中的 TPU 本构模型也在其中。引用两段关于她的介绍：

Mary C. Boyce is Dean of Engineering at The Fu Foundation School of Engineering and Applied Science at Columbia University in the City of New York and the Morris A. and Alma Schapiro Professor of Engineering. Prior to joining Columbia, Dean Boyce served on the faculty of the Massachusetts Institute of Technology (MIT) for over 25 years, leading the Mechanical Engineering Department from 2008 to 2013.

Her research focuses on materials and mechanics, particularly in the areas on multi-scale and nonlinear mechanics of polymers and soft composites, both those that are man-made and those formed naturally. Her leadership in the field of mechanics of materials has expanded understanding of the interplay between micro-geometry and the inherent physical behavior of a material, which has led to innovative hybrid material designs with novel properties. Her research has been documented in over 170 archival journal articles spanning materials, mechanics, and physics. She has mentored over 40 M.S. thesis students and over 25 Ph.D. students. She has been widely recognized for her scholarly contributions to the field, including election as a fellow of the American Society of Mechanical Engineers, the American Academy of Arts and Sciences, and the National Academy of Engineering.

AB 模型适用于多种高分子材料，尤其是存在应变软化的材料，可以描述无定形高分子在大变形情况下的各向异性力学行为，即在不同变形情况下，例如单轴压缩、平面应变，其力学行为不同。

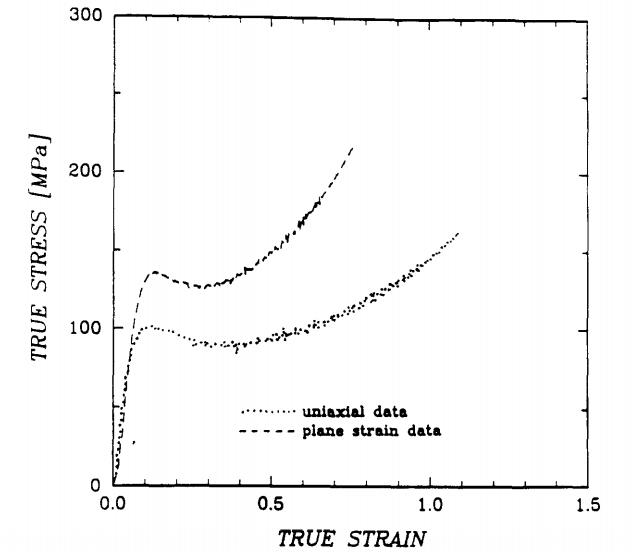PMMA 材料在两种压缩变形下的应力应变曲线

AB 本构模型

类似于 TPU 本构模型，AB 模型也由三元素组成，如图2所示。但 AB 本构模型适用于单相材料，不存在两相变换的情况，所以要简单一些。主要公式有

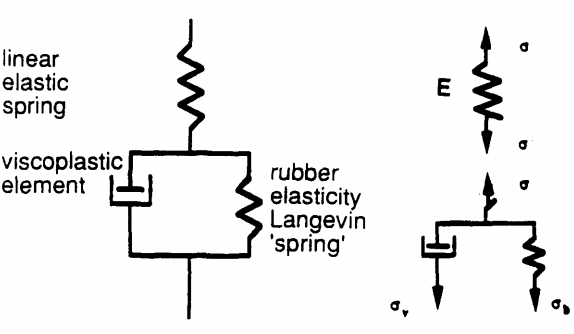AB 本构模型
\begin{equation*} F=F^eF^p \\ F^p=F^{ps}=F^{pd} \\ L=\dot{F}F^{-1}=\dot{F}^e(F^e)^{-1}+F^e\dot{F}^p(F^p)^{-1}(F^e)^{-1}=D+W \\ L^p=\dot{F}^p(F^p)^{-1}=D^p+W^p \\ L^e=\dot{F}^e(F^e)^{-1} \\ L=L^e+F^eL^p(F^e)^{-1} \\ T=T^e=T^p \\ T^p=T^{ps}+T^{pd} \\ T^e=\frac{1}{J^{e}}\mathbf{L}^e[lnV^{e}] \\ J^{e}=det(F^{e}) \\ T^{ps}=\frac{\mu_r}{3J^{ps}}\frac{\sqrt{N}}{\lambda_{chain}}\mathscr{L}^{-1}(\frac{\lambda_{chain}}{\sqrt{N}}){\bar{B}^{ps}}^\prime \\ J^{ps}=det(F^{ps})=det(F^{p})=1 \\ \bar{F}^{ps}=(J^{ps})^{-1/3}F^{ps}=F^{ps}=F^p \\ \bar{B}^{ps}=\bar{F}^{ps}(\bar{F}^{ps})^T=F^p(F^p)^T \\ {\bar{B}^{ps}}^\prime=dev(\bar{B}^{ps}) \\ W^{p}=0 \\ D^p=D^{pd}=\frac{\dot{\gamma}^{pd}}{\sqrt{2}\tau^{pd}}{\bar{T}^{pd}}^\prime \\ \tau^{pd}=[\frac{1}{2}{\bar{T}^{pd}}^\prime{\bar{T}^{pd}}^\prime]^{1/2} \\ \bar{T}^{pd}=T^e-\frac{1}{J^e}F^eT^{ps}(F^e)^T \\ {\bar{T}^{pd}}^\prime=dev(\bar{T}^{pd}) \\ \dot{\gamma}^{pd}=\dot{\gamma}_0exp[-\frac{\Delta G}{k\Theta}(1-\frac{\tau^{pd}}{s})] \\ \dot{s}=h(1-\frac{s}{s_{ss}})\dot{\gamma}^{pd} \end{equation*}

总的变形梯度可以分解为弹性变形梯度和塑性变形梯度，前者决定了线弹性弹簧的应力，而后者能够决定超弹性弹簧的应力，两者之差即为阻尼上的应力，该应力控制了塑性变形梯度的变化率。有一点我不是很明白，为什么要这样计算 $\bar{T}^{pd}$？这一点与 TPU 本构模型中的不一致。因为 $D^{pd}$ 是在松弛状态下的，所以其驱动力 ${\bar{T}^{pd}}^\prime$ 应该也是在松弛状态下的。我认为应该是

\begin{equation*} \bar{T}^{pd}=(R^e)^T(T^e-T^{ps})R^e \end{equation*}

除此以外，与 TPU 本构模型还是很相似。其中，$s$ 是来描述应变软化现象的，随着加载其值不断减小。在 $\tau^{pd}$ 不变的情况下，$\dot{\gamma}^{pd}$ 则不断增加，使得 $F^p$ 增大，而 $F^e$ 减小，从而应力下降，所以能够描述在加载过程中应力在中途会下降的试验现象。材料参数有 $E$，$v$，$\mu_r$，$N$，$A$，$h$，$s_{ss}$，$\dot{\gamma}_0$，$\Delta G$。

VUMAT 实现方法

在VUMAT中，已知的是当前时刻以及下一个时刻的变形梯度 $F_{n}$ 和 $F_{n+1}$，重点是计算 $F^{pd}$，可以采用4阶龙格库塔法来求解。详细来说，对于 $F^{pd}$，则需要将总的变形梯度分为两部分，前一部分为 $F^{e}$，决定了线弹性弹簧的应力，该应力控制了 $F^{pd}$ 的变化率。大致的公式为

\begin{equation*} \dot{F}^{pd}=D^{pd}F^{pd}=f(F,F^{pd}) \\ k_1=f(F_n,F^{pd}_n) \\ k_2=f(F_{n+1/2},F^{pd}_n+k_1*\frac{dt}{2}) \\ k_3=f(F_{n+1/2},F^{pd}_n+k_2*\frac{dt}{2}) \\ k_4=f(F_{n+1},F^{pd}_n+k_3*dt) \\ F^{pd}_{n+1}=F^{pd}_{n}+(k_1+2*k_2+2*k_3+k_4)*\frac{dt}{6} \\ F_{n+1/2}=(F_{n}+F_{n+1})/2 \end{equation*}