Abaqus周期边界条件的设置

Mar 19, 2018 • 9 min read

周期边界条件是一类常见的边界条件，在复合材料中通常选取一个代表性体积单元（RVE），通过计算该单元的变形或应力来得到整个材料的性能。在Abaqus中不能直接设置周期边界条件，需要对边界上的节点进行多点约束（MPC）。

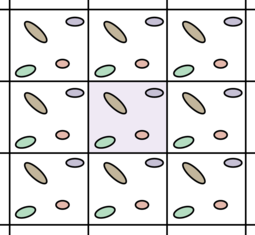周期性结构

以上述2D结构为例具体介绍周期边界条件的设置。假设该结构在垂直方向上（也即y方向）施加应变载荷 $\epsilon$，而在其他方向上没有载荷。把中间的一块区域提取出来作为结构的RVE，该单元的四个边界上需要施加相应的边界条件：

在x方向上的边界上 $\Gamma_l$ 和 $\Gamma_r$ 存在应变载荷；
在y方向上的边界上 $\Gamma_b$ 和 $\Gamma_t$ 存在周期边界。

假设在 $\Gamma_l$ 和 $\Gamma_r$ 边界上配对的两点为 $i$ 和 $j$，其位移分别为 $u_i$，$v_i$，$u_j$ 和 $v_j$，则上述第一个条件可以写为：

\begin{equation*} u_i-u_j=u_{Ref1}\\ v_i-v_j=v_{Ref1} \end{equation*}

假设在 $\Gamma_b$ 和 $\Gamma_t$ 边界上配对的两点为 $k$ 和 $l$，其位移分别为 $u_k$，$v_k$，$u_l$ 和 $v_l$，则上述第二个条件可以写为：

\begin{equation*} u_k-u_l=u_{Ref2}\\ v_k-v_l=v_{Ref2} \end{equation*}

其中 $u_{Ref1}$，$v_{Ref1}$，$u_{Ref2}$ 和 $v_{Ref2}$ 是两个参考点Ref1和Ref2的位移。由于在y方向上存在应变载荷，所以两个参考点的y方向位移可以根据应变求得

\begin{equation*} v_{Ref1}=\epsilon*(y_i-y_j)\\ v_{Ref2}=\epsilon*(y_k-y_l) \end{equation*}

上述y方向位移载荷施加在两个参考点上。由于在x方向上没有位移约束，所以参考点的x方向位移没有限制。需要注意的是，如果建立了MPC但是没有限制参考点的位移，那么结构在该方向上是存在变形的，如果将其参考点的位移设置为0，那么在该方向上的位移为0，即结构不会膨胀或收缩。

在Abaqus中设置上述边界条件有如下步骤：

确定两个参考点；
确定四个边界上的节点编号，分别储存在left，right，bottom和top四个数组中；
在对应的两个边界上例如left和right，以及bottom和top中，寻找距离最近的两个节点作为一对，设置边界条件。具体方法是采用双重循环，在left中任取一个节点M，然后遍历right中的所有节点，找到和节点M距离最近的节点，即为与之配对的节点N。bottom和top也采用类似操作；
在load模块中设置两个参考点的位移约束。

2D算例

如下图所示的周期性结构承受y方向上的压缩位移载荷，可以采用两种方法来计算其结构变形，并且两者结果可以进行对比。

2D周期性结构

整体模型计算

这种方法比较简单，在水平和垂直方向的应变如下两图所示：

整体结构的应变

其中心区域的变形如下图所示：

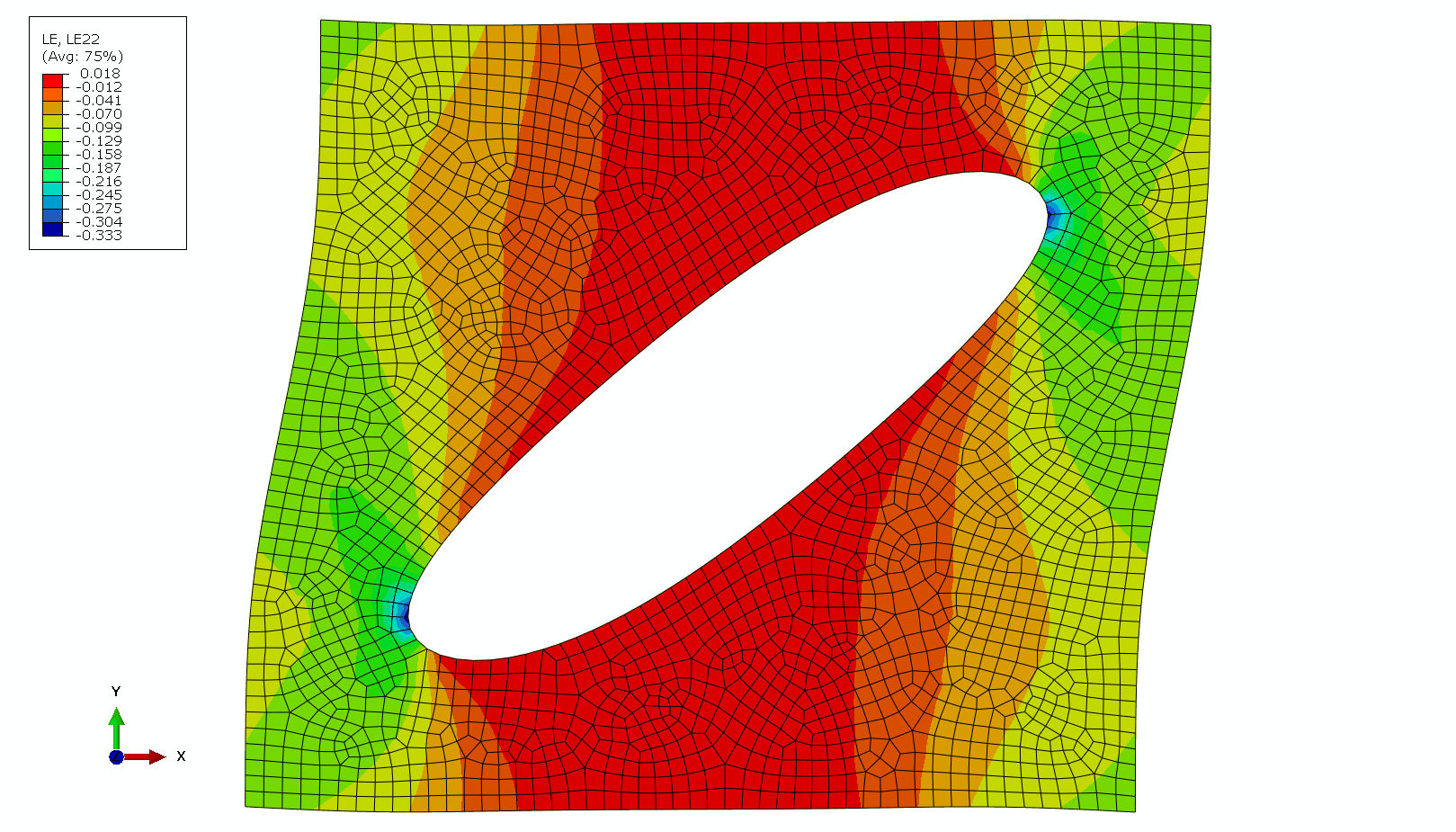中心单元的应变

周期边界模型计算

采用周期边界模型进行计算，网格数减少，计算速度会变快，其应变结果如下图所示：

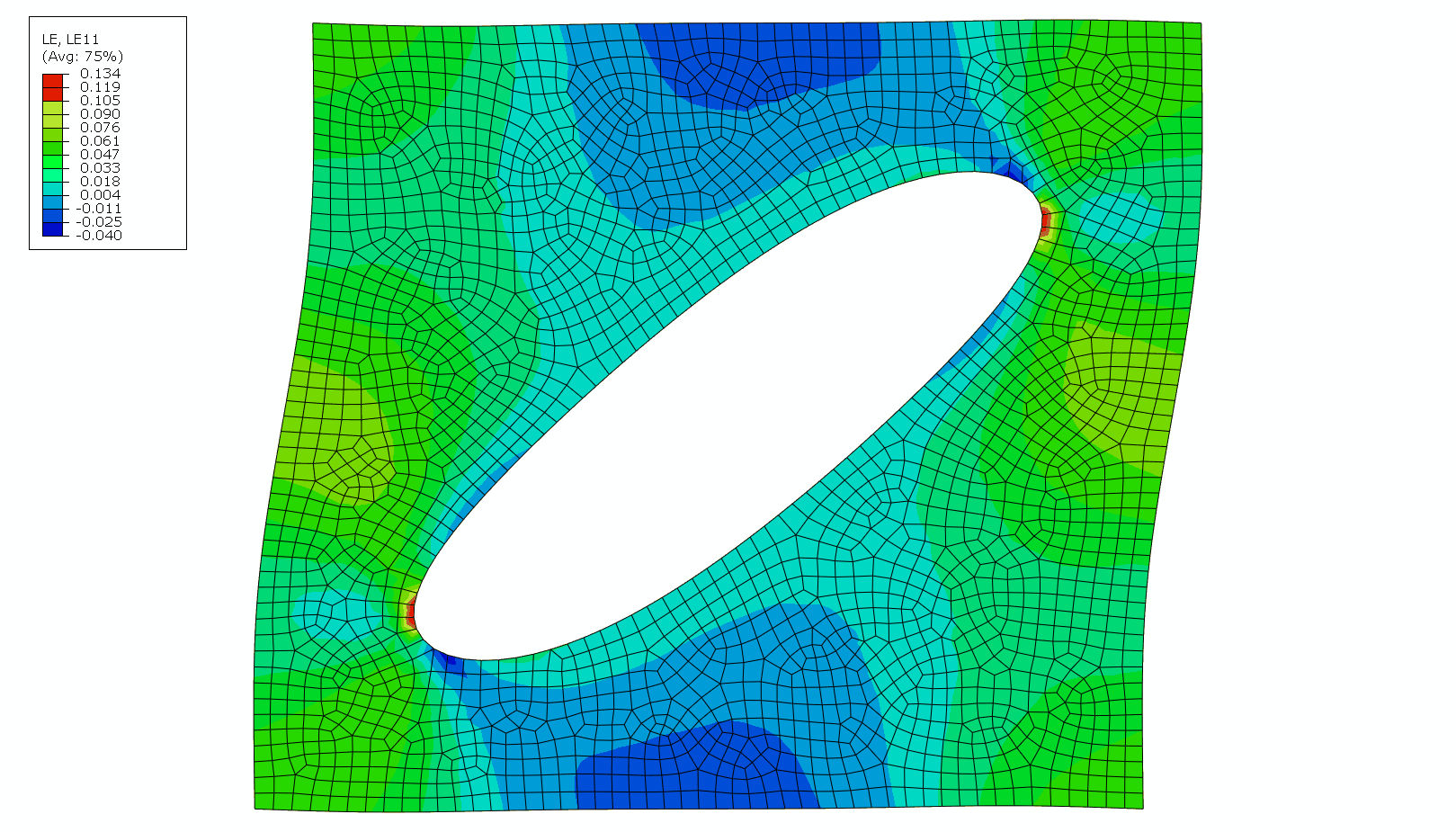
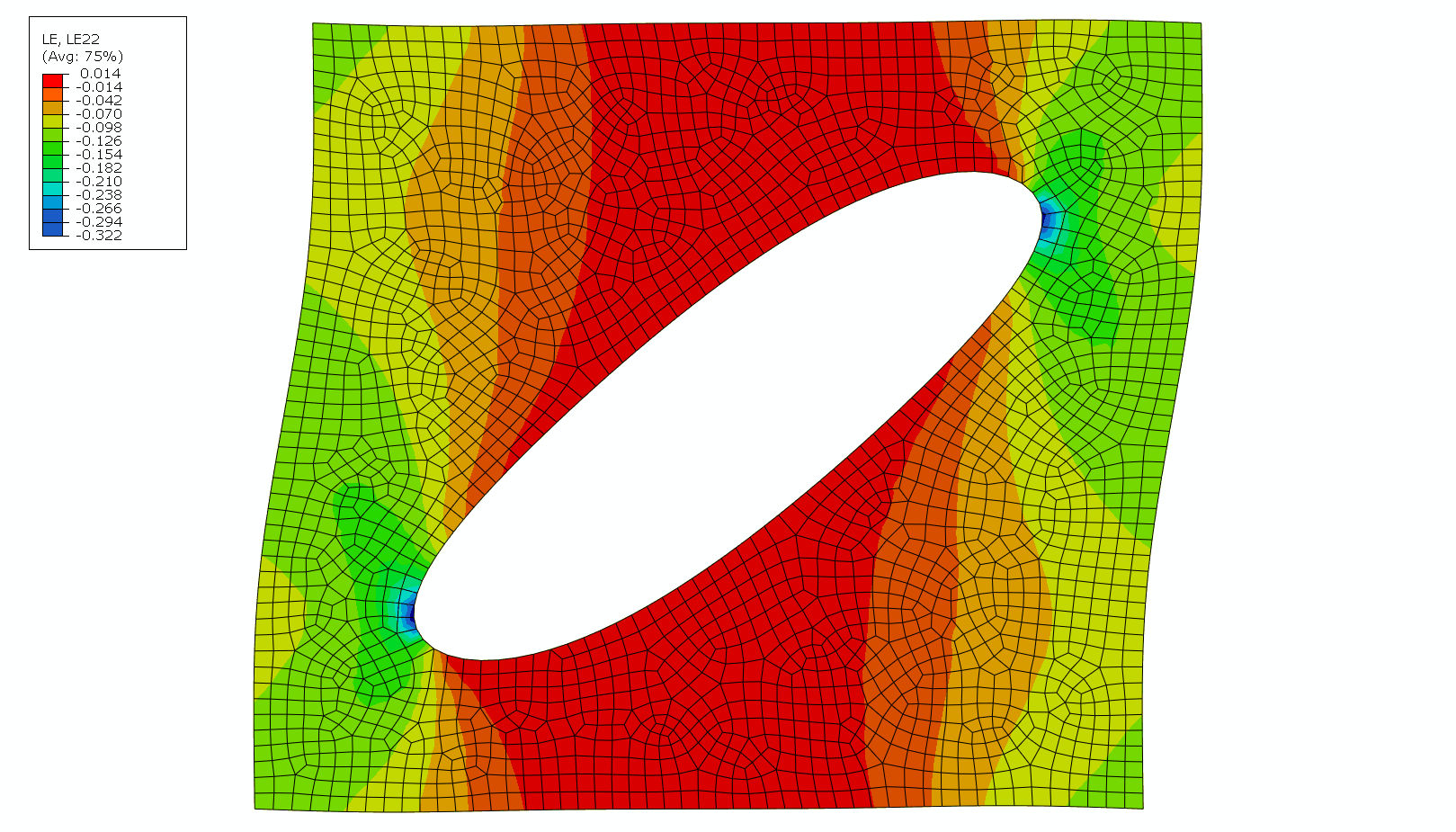周期边界模型的应变

通过对比可知，两种方法的计算结果很近似，从而验证了周期边界设置的正确性。不够精确。

以下是3D情况下周期边界条件设置的python代码：

# -*- coding: cp936 -*- 
# 3D PBC  
from abaqus import *
from abaqusConstants import *
from caeModules import *
from driverUtils import executeOnCaeStartup
executeOnCaeStartup()
from interaction import *   #定义多点约束条件-----MPC
fields=(('x min:','0.0'),('x max:','1.0'),('y min:','0.0'),('y max:','1.0'),('z min:','0.0'),('z max:','1.0'))
xmin,xmax,ymin,ymax,zmin,zmax=getInputs(fields=fields,label="Input the parameters")
xmin=float(xmin);xmax=float(xmax);ymin=float(ymin);ymax=float(ymax);zmin=float(zmin);zmax=float(zmax)

tor=0.001

m=mdb.models['Model-3']
r=m.rootAssembly

#找到参考点
refpoints=r.referencePoints
for i in range(len(refpoints)):
    r.Set(name='Ref-'+str(i+1),referencePoints=(refpoints.values()[i],))
    
#找到边界节点    
node=r.instances['Part-1-1'].nodes
ne1=[]
ne2=[]
ne3=[]
ne4=[] 
ne5=[]
ne6=[]   
for i in range(len(node)):
    x=node[i].coordinates[0]
    y=node[i].coordinates[1]
    z=node[i].coordinates[2]
    if (abs(x-xmin)<tor):
        ne1.append(i)
    if (abs(x-xmax)<tor):
        ne2.append(i)
    if (abs(y-ymin)<tor):
        ne3.append(i)
    if (abs(y-ymax)<tor):
        ne4.append(i) 
    if (abs(z-zmin)<tor):
        ne5.append(i)
    if (abs(z-zmax)<tor):
        ne6.append(i)   

#定义LR边界节点的PBC
for n in range(min(len(ne1),len(ne2))):
    x0=node[ne1[n]].coordinates[0]
    y0=node[ne1[n]].coordinates[1]
    z0=node[ne1[n]].coordinates[2]
    r.Set(nodes=node[ne1[n]:ne1[n]+1],name='Set-L-'+str(n+1))
    mindistance=sqrt((xmin-xmax)**2+(ymin-ymax)**2+(zmin-zmax)**2)*2
    index=0
    for j in range(len(ne2)):
        x1=node[ne2[j]].coordinates[0]
        y1=node[ne2[j]].coordinates[1]
        z1=node[ne2[j]].coordinates[2]
        distance=sqrt((x0-x1)**2+(y0-y1)**2+(z0-z1)**2)
        if (distance < mindistance):
            mindistance=distance
            index=j
    r.Set(nodes=node[ne2[index]:ne2[index]+1],name='Set-R-'+str(n+1))
    m.Equation(name='Eq-LR-X-'+str(n+1),terms=((1,'Set-L-'+str(n+1),1),(-1,'Ref-1',1),(-1,'Set-R-'+str(n+1),1)))
    m.Equation(name='Eq-LR-Y-'+str(n+1),terms=((1,'Set-L-'+str(n+1),2),(-1,'Ref-1',2),(-1,'Set-R-'+str(n+1),2)))
    m.Equation(name='Eq-LR-Z-'+str(n+1),terms=((1,'Set-L-'+str(n+1),3),(-1,'Ref-1',3),(-1,'Set-R-'+str(n+1),3)))

#定义BT边界节点的PBC
for n in range(min(len(ne3),len(ne4))):
    x0=node[ne3[n]].coordinates[0] 
    y0=node[ne3[n]].coordinates[1]
    z0=node[ne3[n]].coordinates[2]
    r.Set(nodes=node[ne3[n]:ne3[n]+1],name='Set-B-'+str(n+1))
    mindistance=sqrt((xmin-xmax)**2+(ymin-ymax)**2+(zmin-zmax)**2)*2
    index=0
    for j in range(len(ne4)):
        x1=node[ne4[j]].coordinates[0]
        y1=node[ne4[j]].coordinates[1]
        z1=node[ne4[j]].coordinates[2]
        distance=sqrt((x0-x1)**2+(y0-y1)**2+(z0-z1)**2)
        if (distance < mindistance):
            mindistance=distance
            index=j                                                                                                                                                                                                          
    r.Set(nodes=node[ne4[index]:ne4[index]+1],name='Set-T-'+str(n+1))
    m.Equation(name='Eq-BT-X-'+str(n+1),terms=((1,'Set-B-'+str(n+1),1),(-1,'Ref-2',1),(-1,'Set-T-'+str(n+1),1)))
    m.Equation(name='Eq-BT-Y-'+str(n+1),terms=((1,'Set-B-'+str(n+1),2),(-1,'Ref-2',2),(-1,'Set-T-'+str(n+1),2)))
    m.Equation(name='Eq-BT-Z-'+str(n+1),terms=((1,'Set-B-'+str(n+1),3),(-1,'Ref-2',3),(-1,'Set-T-'+str(n+1),3)))
    
#定义FN边界节点的PBC
for n in range(min(len(ne5),len(ne6))):
    x0=node[ne5[n]].coordinates[0] 
    y0=node[ne5[n]].coordinates[1]
    z0=node[ne5[n]].coordinates[2]
    r.Set(nodes=node[ne5[n]:ne5[n]+1],name='Set-F-'+str(n+1))
    mindistance=sqrt((xmin-xmax)**2+(ymin-ymax)**2+(zmin-zmax)**2)*2
    index=0
    for j in range(len(ne6)):
        x1=node[ne6[j]].coordinates[0]
        y1=node[ne6[j]].coordinates[1]
        z1=node[ne6[j]].coordinates[2]
        distance=sqrt((x0-x1)**2+(y0-y1)**2+(z0-z1)**2)
        if (distance < mindistance):
            mindistance=distance
            index=j                                                                                                                                                                                                          
    r.Set(nodes=node[ne6[index]:ne6[index]+1],name='Set-N-'+str(n+1))
    m.Equation(name='Eq-FN-X-'+str(n+1),terms=((1,'Set-F-'+str(n+1),1),(-1,'Ref-3',1),(-1,'Set-N-'+str(n+1),1)))
    m.Equation(name='Eq-FN-Y-'+str(n+1),terms=((1,'Set-F-'+str(n+1),2),(-1,'Ref-3',2),(-1,'Set-N-'+str(n+1),2)))
    m.Equation(name='Eq-FN-Z-'+str(n+1),terms=((1,'Set-F-'+str(n+1),3),(-1,'Ref-3',3),(-1,'Set-N-'+str(n+1),3)))

Next post ›

‹ Previous post