读书笔记 1 - 连续介质力学

Jan 7, 2016 • 1 min read

最近在读 Ted Belytschko 等人编写的《Nonlinear Finite Elemens for Continua and Structures, Second Edition》，刚读完第三章连续介质力学，对此有些体会，但更多的是疑惑。故先记录如下，以免日后忘却。

虽然是固体力学专业，但我以前没有系统地学过连续介质力学，快毕业的时候看完这一章，突然觉得有点惭愧啊。以前零零碎碎地学习材料力学、弹性力学、塑性力学以及结构动力学等知识，现在感觉是以管窥豹，对固体力学没有一个较为全面的、脉络式的认识。这些力学是固体力学的一个个子集，分别对某个具体的情况进行分析，包含了一系列的假设。其中，最重要的一个是小变形假设，在这个假设下，方程或公式可以得到简化，因此便于理解和掌握。所以以往的认识是针对一个特殊情况的，不适用于整个情况。当然这个状态是可以理解的，学习的过程应该是由易到难，尤其是工科生。

这一章的内容不多，但比较基础。从材料的变形开始，提出两种描述方式，即 Lagrange 描述和 Euler 描述，然后介绍在这两种描述下的应变度量，应力度量，接着是两种描述下的守恒方程，最后介绍了变形梯度的极分解以及客观率（框架不变性）。在这一过程中，考虑到大变形、旋转和刚体运动，应力应变度量与以前的小变形情况有较大的不同。该章写的通俗易懂，讲解令人印象深刻，公式推导简洁明了，细节处的详细推导让人能够更加容易理解。通过阅读这一章的内容，我对连续介质力学有如下的体会：

如何描述材料的运动和变形是一个重要的议题。通过分析变形前、后两种形态，提出一种描述这种变形的函数关系，$x=\phi(X,t)$。其中，$X$，$x$分别指的是材料点在变形前后形态下的位置矢量。然后可以引出两种描述形式，即 Lagrange 描述和 Euler 描述。根据 $x$ 和 $X$ 可以定义位移、速度和加速度，在对 Euler 描述的位移和速度求时间导数的时候，引出了两种导数，即材料时间导数和空间时间导数。接着引入了一个重要的概念，即变形梯度 $F$，$dx=F\dot{} dX$。

\begin{equation*} \frac{Dv(x,t)}{Dt}=\frac{\partial v(x,t)}{\partial t}+v\dot{} \Delta v \end{equation*}

介绍了刚体转动以及坐标转换，这一点比较有意思。此时，$x=R(t)X+x_T(t)$，即 $F=R$。其中 $R$ 为单位正交阵。在坐标转换时，对向量只需左乘转换矩阵 $R$ 即可，对于二阶张量，则需要左乘转置的转换矩阵，然后再右乘转换矩阵。在 Euler 描述下引出了角速度张量 $\Omega=\dot{R}\dot{}R^T$，该张量为反对称张量。
两种应变度量，即 Green 应变 $E$ 和变形率 $D$。其中，Green 应变是在 Lagrange 描述下定义的，而变形率是在 Euler 描述下定义的。两者之间存在一定的关系，而且都可以通过变形梯度来得到。

\begin{equation*} E=\frac{1}{2}(F^T\dot{}F-I)\\ L=\frac{\partial v}{\partial x}=\dot{F}\dot{}F^{-1}\\ L=D+W\\ D=\frac{1}{2}(L+L^T)\\ W=\frac{1}{2}(L-L^T)\\ D=F^{-T}\dot{}\dot{E}\dot{}F^{-1} \end{equation*}

三种应力度量，即 Cauchy 应力 $\sigma$、名义应力 $P$ 和 PK2 应力 $S$。其定义分别为 $df=n\dot{}\sigma d\Gamma=n_0\dot{}Pd\Gamma_0=F\dot{}(n_0\dot{}Sd\Gamma_0)$。除此之外，还有两种应力度量，即旋转应力和 Kirchhoff 应力。这五者之间存在相互转换，如图1所示。

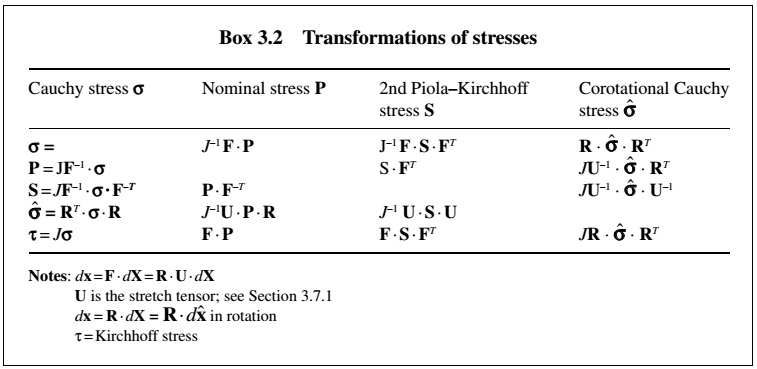应力转换关系

在两种描述下的守恒方程，包括质量守恒、线动量守恒、角动量守恒以及能量守恒定律，如图2所示。其中，Cauchy 应力 $\sigma$ 和变形率 $D$、PK2 应力 $S$和 Green 应变率 $\dot{E}$、名义应力 $P$ 和变形梯度率 $\dot{F}$ 是功共轭的。

守恒方程

变形梯度的极分解以及框架不变性。任意变形梯度均可以表示为一个旋转矩阵和一个对称张量的乘积，即 $F=R\dot{}U=V\dot{}R$，$U=(F^T\dot{}F)^{1/2}$。关于框架不变性，又称之为客观率，我的理解是由于 Euler 描述中的张量在不同的参考系中需要进行坐标变换，而 Lagrange 描述下的张量不需要进行坐标变换。因而，Euler 型张量的材料时间导数不满足坐标转换条件，即不是一个客观性张量。但是，对于本构模型，其基本原理包含了客观性原理。所以，对于 Euler 型张量的材料时间导数需要考虑坐标的旋转。三种客观率如图3所示，本构模型中的应力率一般为 Cauchy 应力的各种客观率。对于旋转应力和 PK2 应力，由于两者考虑到了材料的转动，所以可以直接用于描述本构模型。

客观率

\begin{equation*} \frac{D\sigma}{Dt}=\sigma^{\nabla}+W\dot{}\sigma+\sigma\dot{}W^T\\ \sigma^{\nabla}=C^{\nabla}:D\\ \dot{\hat{\sigma}}=\hat{C}^{\hat{\sigma}}:\hat{D}\\ \dot{S}=C^{SE}:\dot{E} \end{equation*}

现在我对这部分内容还有很多理解不清晰的地方，这些疑问有：

为什么变形梯度的行列式 $J=det(F)$ 会将两种形态下的积分关联起来？

\begin{equation*} \int_{\Omega}f(x,t)\,d\Omega=\int_{\Omega_0}Jf(\phi(X,t),t)\,d\Omega_0 \end{equation*}

为什么反对称张量可以有如下的表示形式？

\begin{equation*} \Omega r=\omega \times r \end{equation*}

在两种描述下推导守恒方程，其目的是为何？

Next post ›

‹ Previous post